Diagrama de Clases

Multiperceptron

Multiadaline

Agentes Inteligentes - Diego Orellana

Podemos definir al agente inteligente como una entidad software que basándose en su propio conocimiento, realiza un conjunto de operaciones destinadas a satisfacer las necesidades de un usuario o de otro programa, bien por iniciativa propia o porque alguno de éstos se lo requiere.

Todos los agentes inteligentes son programas, pero no todos los programas que realizan búsquedas son agentes inteligentes. Los agentes en sí mismos pueden ser considerados como entidades individuales (partes de programa que tienen control sobre sus propias vidas y movimientos). Continuamente están realizando procesos que les indican qué hacer y cómo. Se comunican con otros agentes para resolver de forma adecuada su trabajo.

De acuerdo con el punto de vista de la inteligencia artificial un agente posee las siguientes propiedades: autonomía, sociabilidad, capacidad de reacción, iniciativa, benevolencia y racionalidad (Wooldridge y Jennings, 1995).

Diagramas de Clase - Diego Orellana

FORMULAS TOPOLOGIAS

Perceptron

net = W´P + b

a= f(net)

e = t-a

Wn = Wa + e.P

bn = ba + e



Tomar en cuenta que si el valor final de net es >= 0 f(net) toma el valor de 1, caso contrario toma el valor de 0.


Las iteraciones se repiten hasta que el valor de e sea equivalente a 0.

Multi-Perceptron

net = WP + b
a= f(net)
e = t-a
Wn = Wa + e.P
bn = ba + e

Tomar en cuenta que si el valor final de net es >= 0 f(net) toma el valor de 1, caso contrario toma el valor de 0.

Las iteraciones se repiten hasta que el valor de e² sea <= a 0.01

Adaline

net = W´P + b
a= f(net)=net
e = t-a
Wn = Wa + e.alpha.P
bn = ba + alpha.e

Las iteraciones se repiten hasta que el valor de e sea <= a 0.01

PANTALLAZOS PROGRAMAS C#

Perceptron

Multiperceptron

Adaline

DIAGRAMAS DE CLASES

Perceptron

Multiperceptron

Adaline

ADALINE

DIAGRAMA DE CLASES ADALINE:FÓRMULAS PARA EL ENTRENAMIENTO:

net=W*P+b

a=f(net)=net

e=t-a

se repite el entrenamiento hasta que eror sea menor o igual a 0,01

MULTIADALINE

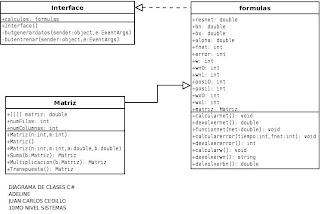
DIAGRAMA DE CLASES MULTIADALINE:

FÓRMULAS PARA EL ENTRENAMIENTO:
net=W*P+b
a=f(net)=net
e=t-a
condición el error es menor o igual a 0,01 se termina el entrenamiento

MULTIPERCEPTRON

DIAGRAMA DE CLASES MULTIPERCEPTRON:

FÓRMULAS PARA EL ENTRENAMIENTO DE LA RED:

son las mismas que se utilizan en el perceptron

con la condición de:

donde este valor de e² es menor igual a 0,01

PERCEPTRON

DIAGRAMA DE CLASES: PERCEPTRON

FÓRMULAS PARA EL ENTRENAMIENTO:
net=(W)'*P+b
a=f(net)

e=t-a
si el error es: e=0 se termina el entrenamiento
caso contrario:
Wn=W+e*P
bn=b+e